Algorithms and Data Structures Series: Hash Maps

This post is part of the algorithms and data structures series, a series of posts where I present the most common data structures and algorithms used in software engineering. In this post, I explain the basics of Hash maps, also known as hash tables or dictionaries.

The Hash map stores data in a key-value pair. Similar to arrays, accessing a piece of data from a position has constant complexity, but the positions on hash maps behave differently. Instead of having sequential numeric indexes, the Hash map allows any type of data to be used as its key. This makes the Hash map one of the best and most used data structures for optimizing algorithms.

Contents

• Behavior
• Hash function
• Collision
• Implementation
  • Hash function
  • Insert
  • Lookup
  • Delete
  • Traverse
• Complexity table
• Choosing hash maps over other data structures
  • When to use
  • When to avoid
• Full hash map implementation
• Sources

Behavior

The main operations implemented by a hash map are setting a value into a key, retrieving the value from a key, and removing a value from a key. Additionally, it can provide other operations like returning all keys from the hash map that can be used to traverse it.

Another peculiarity of hash maps compared to arrays is that it does not have order. Traversing a map will not bring the values in the same order they were added. There are some implementations that keep the order of the added keys, but with the cost of additional space.

Hash function

This data structure is called a Hash map due to how the keys and values are resolved and stored internally. It makes use of a hash function and an array of "buckets". The hash function receives the provided key and transforms it into a number in a way that every time the same key is provided, the same number is returned. This number is then used as the index of the internal array of "buckets". For the bucket, another data structure is used, like another array or a linked list and it is used to store the key-value pair.

The process of inserting a value into a Hash map works as follows:

1. The hash map receives the key and value to be stored
2. The key is given to the hash function and the bucket index is resolved
3. The key-value pair is inserted in the bucket corresponding to the resolved index

Retrieving the value from a Hash map follows a similar process:

1. The hash map receives a key
2. The key is given to the hash function and the bucket index is resolved
3. The value of the bucket is returned based on the resolved index

Here is a visual representation of how values are stored:

Source: https://en.wikipedia.org/wiki/Hash_table

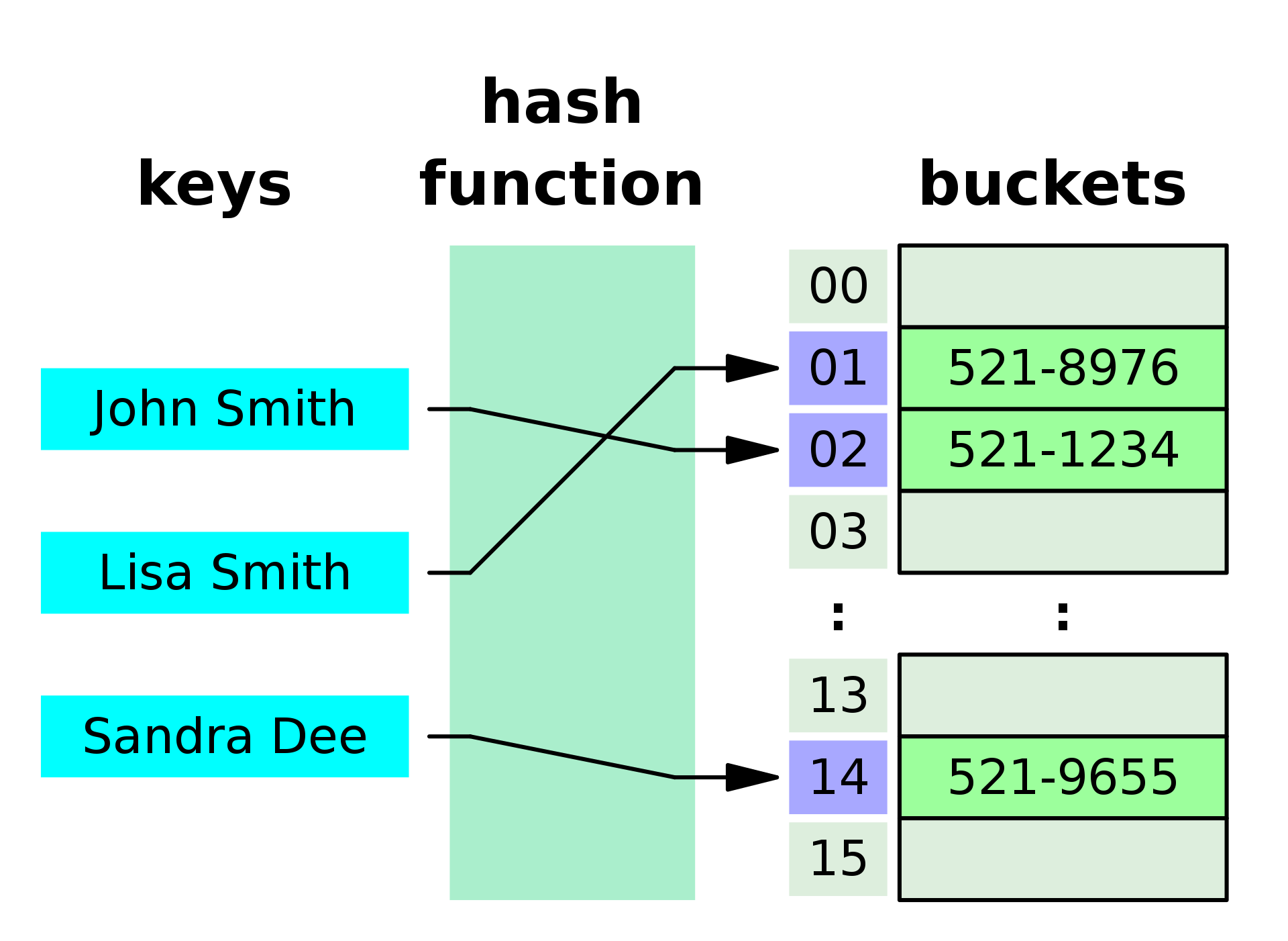
Collision

Sometimes, two different keys can return the same result after been passed to the hash function. We call this collision. To solve this problem, the buckets don't contain the values directly, but lists of values of the same hashing result. This list can be implemented using data structures like dynamic arrays or linked lists. There are other collision resolution techniques and you can check some of them on Hash table - Wikipedia.

Implementation

Now let's start with our Hash map implementation. The code examples are written using the Go programming language, but they are simple enough that can be applied to any language.

First, we start with our HashMap type and constructor function:

type BucketItem[T any] struct {
  key   string
  value T
}

type Bucket[T any] []*BucketItem[T]

type HashMap[T any] struct {
  buckets []Bucket[T]
}

func NewHashMap[T any]() *HashMap[T] {
  return &HashMap[T]{
    buckets: make([]Bucket[T], 1000),
  }
}

The HashMap type contains a list of Bucket types. Each Bucket is a list of BucketItem types. The BucketItem stores a key and a value. The value can be of any type using Go's generics. The key is of the string type. This decision was made to make the hash function simpler. On the native map implementation of Go, the key can be of any type.

The NewHashMap function returns a pointer to a HashMap. The buckets argument is initialized with a length of 1000. This length is important to the hash function as it uses it to resolve the indexes where values are set.

Hash function

The hash function is used by the "insert", "lookup", and "delete" operations. It gets a key and returns a number corresponding to the index of the internal buckets list. Here is the implementation:

func (h *HashMap[T]) hashKey(value string) int {
  hash := 0

  for i, chr := range value {
    hash = (hash + int(chr)*i) % len(h.buckets)
  }

  return hash
}

This is a very simple implementation of a hash function where it uses the code points of each character of the given key together with the length of the internal buckets list as a range to resolve the appropriate bucket index. Native hash map implementations use different hash function algorithms.

This hash function as the time complexity of O(n) where n is the size of the key. Although this is not a constant complexity, it will be ignored in the complexity calculation of the hash map operations that use it. The reason for that is that key lengths are usually very small in comparison to the number of items that are stored in the Hash map.

Insert

Now let's implement the first operation of our hash map. To insert items, we use the Set method. It receives the key and the value as arguments. Here is the implementation:

func (h *HashMap[T]) Set(key string, value T) {
  bucketIndex := h.hashKey(key)
  h.ensureBucketExists(bucketIndex)

  item := h.findBucketItem(bucketIndex, key)
  if item != nil {
    item.value = value
  } else {
    h.appendNewBucketItem(bucketIndex, key, value)
  }
}

func (h *HashMap[T]) ensureBucketExists(bucketIindex int) {
  if h.buckets[bucketIindex] == nil {
    h.buckets[bucketIindex] = make(Bucket[T], 0, 1)
  }
}

func (h *HashMap[T]) findBucketItem(bucketIndex int, key string) *BucketItem[T] {
  for _, item := range h.buckets[bucketIndex] {
    if item.key == key {
      return item
    }
  }
  return nil
}

func (h *HashMap[T]) appendNewBucketItem(bucketIndex int, key string, value T) {
  item := &BucketItem[T]{key, value}
  h.buckets[bucketIndex] = append(h.buckets[bucketIndex], item)
}

The first thing to do is to get the bucket index by calling the hashKey method. With this index in hand, we need to ensure that a bucket exists on that position. One is created otherwise. Each bucket contains a list of bucket items, so the next step is to check if the key being inserted already belongs to an item in the bucket. In other words, if there is already an item with that key in the hash map. If it exists, the value is replaced. If not, a new BucketItem is appended to the bucket.

Notice that the bucket is a list (slice) on this example. Many hash map implementation uses a linked list here so there is no time lost with the list internal expansions. Although there is some performance lost here, the list fits well for this example.

In an ideal scenario, each bucket has only one item, that would make loops in the bucket trivial. But sometimes, depending on the keys given to the hash function, different keys return the same bucket position. When that happens we say we have a collision. That is the reason the bucket is a list so we can store more than one key in the same bucket.

The time complexity of the Set method is in average O(1) with a worst case scenario of O(n) when all the keys resolve to the same bucket.

Lookup

Hash maps are all about looking up by key. We can perform this operation with the Get method. Here is how it can be implemented:

func (h *HashMap[T]) Get(key string) T {
  bucketIndex := h.hashKey(key)

  if h.bucketExists(bucketIndex) {
    item := h.findBucketItem(bucketIndex, key)

    if item != nil {
      return item.value
    }
  }

  return h.emptyValue()
}

func (h *HashMap[T]) bucketExists(index int) bool {
  return h.buckets[index] != nil
}

func (h *HashMap[T]) findBucketItem(bucketIndex int, key string) *BucketItem[T] {
  for _, item := range h.buckets[bucketIndex] {
    if item.key == key {
      return item
    }
  }
  return nil
}

func (h *HashMap[T]) emptyValue() T {
  var value T
  return value
}

The Get method starts by calling hashKey to resolve the index of the bucket where the value for the given key is supposelly stored. It then checks if a bucket exists on that position. If so, we need to look for the correct item inside of the bucket. This is done by looping through all items until an item with the corresponding key is found. If the item exists its value is returned. Otherwise, we return an empty value.

Like Set, the time complexity of the Get method is in average O(1) with a worst case scenario of O(n).

Delete

Removing an item from the hash map follows a similar pattern:

func (h *HashMap[T]) Delete(key string) {
  bucketIndex := h.hashKey(key)

  if h.bucketExists(bucketIndex) {
    for i, item := range h.buckets[bucketIndex] {
      if item.key == key {
        h.removeItem(bucketIndex, i)
        return
      }
    }
  }
}

func (h *HashMap[T]) bucketExists(index int) bool {
  return h.buckets[index] != nil
}

func (h *HashMap[T]) removeItem(bucketIndex, itemIndex int) {
  bucket := h.buckets[bucketIndex]
  h.buckets[bucketIndex] = append(bucket[:itemIndex], bucket[itemIndex+1:]...)
}

We start by hashing the key and resolving the bucket index. With that index, we check if the bucket exists. If so, we loop through the items of the bucket and remove the item that corresponds to the key.

The time complexity of the Delete method is in average O(1) with a worst case of O(n).

Traverse

To traverse a hash map we need to get all the keys that were inserted in the map. With the keys in hand we can easily get all the values. Hehe is how we implement a Keys method:

func (h *HashMap[T]) Keys() []string {
  keys := []string{}

  for _, bucket := range h.buckets {
    if bucket != nil {
      for _, item := range bucket {
        keys = append(keys, item.key)
      }
    }
  }

  return keys
}

The Keys method loops through all the buckets. If a bucket is found, it loops through all its items getting their keys and adding them to the result slice. As we don't know in which positions of the bucket list the items are stored, we need to loop through all buckets. This gives us a time complexity of O(k) where k is the length of the internal bucket storage.

There are ways of optimizing this operation, for example, we could store all the inserted keys in an extra list and whenever the Keys method gets called we simply return this list. This would make the time complexity of the Keys method be O(1), but it would increate the memory required for the whole hash map. It also changes the Delete method complexity from O(1) to O(n) as the keys need to be removed also from the internal list.

Complexity table

Here is the time complexity table for the operations we just saw:

Operation	Complexity
Insert	O(1)
Lookup	O(1)
Delete	O(1)
Traverse	O(k) where k is the max capacity of buckets

Choosing hash maps over other data structures

The Hash map fast operations make it a very useful data structure. It is frequently used for optimizing many algorithms with the usage of the memoization technique where we take advantage of the fast lookups to cache values for use during the algorithm process. A Hash map is very optimized for its three main operations: insert, lookup, and delete. As long as these are the required operations for the algorithm, the hash map is a very good choice.

Here is what we should consider when choosing or avoiding hash maps in our algorithms:

When to use

• Fast insertions are needed
• Fast lookups are needed
• Fast deletions are needed

When to avoid

• Insertion order is required
• Traversing is needed

Full hash map implementation

type BucketItem[T any] struct {
  key   string
  value T
}

type Bucket[T any] []*BucketItem[T]

type HashMap[T any] struct {
  buckets []Bucket[T]
}

func NewHashMap[T any]() *HashMap[T] {
  return &HashMap[T]{
    buckets: make([]Bucket[T], 1000),
  }
}

func (h *HashMap[T]) Set(key string, value T) {
  bucketIndex := h.hashKey(key)
  h.ensureBucketExists(bucketIndex)

  item := h.findBucketItem(bucketIndex, key)
  if item != nil {
    item.value = value
  } else {
    h.appendNewBucketItem(bucketIndex, key, value)
  }
}

func (h *HashMap[T]) hashKey(value string) int {
  hash := 0

  for i, chr := range value {
    hash = (hash + int(chr)*i) % len(h.buckets)
  }

  return hash
}

func (h *HashMap[T]) ensureBucketExists(bucketIindex int) {
  if h.buckets[bucketIindex] == nil {
    h.buckets[bucketIindex] = make(Bucket[T], 0, 1)
  }
}

func (h *HashMap[T]) findBucketItem(bucketIndex int, key string) *BucketItem[T] {
  for _, item := range h.buckets[bucketIndex] {
    if item.key == key {
      return item
    }
  }
  return nil
}

func (h *HashMap[T]) appendNewBucketItem(bucketIndex int, key string, value T) {
  item := &BucketItem[T]{key, value}
  h.buckets[bucketIndex] = append(h.buckets[bucketIndex], item)
}

func (h *HashMap[T]) Get(key string) T {
  bucketIndex := h.hashKey(key)

  if h.bucketExists(bucketIndex) {
    item := h.findBucketItem(bucketIndex, key)

    if item != nil {
      return item.value
    }
  }

  return h.emptyValue()
}

func (h *HashMap[T]) bucketExists(index int) bool {
  return h.buckets[index] != nil
}

func (h *HashMap[T]) emptyValue() T {
  var value T
  return value
}

func (h *HashMap[T]) Delete(key string) {
  bucketIndex := h.hashKey(key)

  if h.bucketExists(bucketIndex) {
    for i, item := range h.buckets[bucketIndex] {
      if item.key == key {
        h.removeItem(bucketIndex, i)
        return
      }
    }
  }
}

func (h *HashMap[T]) removeItem(bucketIndex, itemIndex int) {
  bucket := h.buckets[bucketIndex]
  h.buckets[bucketIndex] = append(bucket[:itemIndex], bucket[itemIndex+1:]...)
}

func (h *HashMap[T]) Keys() []string {
  keys := []string{}

  for _, bucket := range h.buckets {
    if bucket != nil {
      for _, item := range bucket {
        keys = append(keys, item.key)
      }
    }
  }

  return keys
}

Sources

• Master the Coding Interview: Data Structures + Algorithms
• Hash table - Wikipedia